-1. Before start
모델의 크기를 크게 만드는 3가지 방법
1. depth 증가
2. width 증가 (= filter 개수 증가)
3. 고해상도 이미지 사용

기존에는 3가지 방법을 수동으로 조절하였기에, 최적을 찾지 못하였다.
EfficientNet은 이 3가지의 최적의 조합을 AutoML을 통해 찾아내고, 수식으로 만든 논문이다.
조합을 효율적으로 만들 수 있도록 하는 compound scaling 방법을 제안하며, NAS 구조 수정을 통해 더 작은 크기의 모델로도 SOTA를 달성한 논문이다.
일반적으로 모델을 scaling하는 방법이란, b,c,d방법을 적절히 조절하는 것을 의미한다.
0.Abstract
- 한정된 자원으로 최대의 효율
- compound coefficient 방법
- 더 작으면서 더 빠르고 더 정확
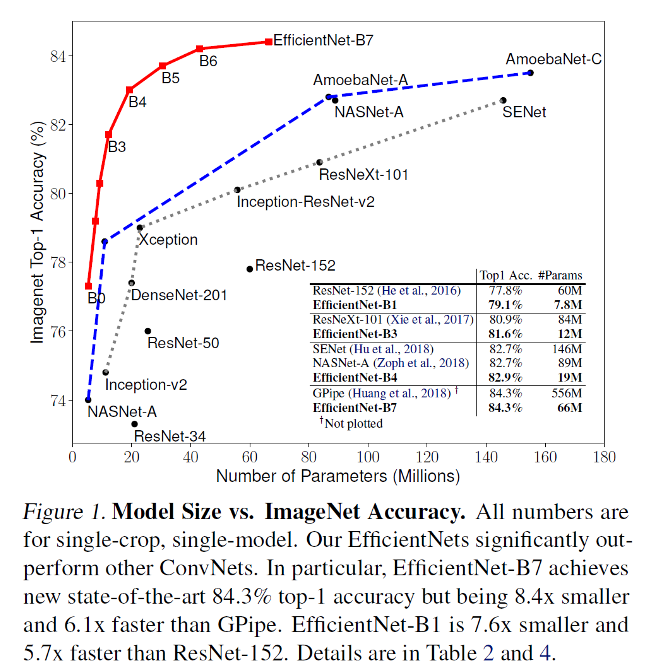
기존 convnet보다 8.4배 작으면서 6.1배 빠르고 더 높은 정확도, compound coefficient 라는 scaling 방법을 제안한다.
1.Introduction
이 논문의 저자들은, 논문의 작성배경을 다음과 같이 말한다.
“ConvNet의 크기를 키우는 것은 널리 쓰이는 방법. 그러나 제대로 된 이해를 바탕으로 이루어지지는 않았던 것 같음. 그래서 scaling하는 방법을 다시 한 번 생각해보고 연구하는 논문을 제안. 그 방법이 compound scaling method.”
2.Related Work
- ConvNet Accuracy : 깊어지고 커질수록 정확도가 상승되는 경향, 그러나 자원 사용률 증가
- ConvNet Efficiency : 깊은 Network는 가끔 over-parameterized 됨. 효율을 높이기 위해 모델을 압축하는 여러 기법이 제안됨 ex) MobileNet
- Model Scaling : 많은 연구가 진행되었으나, 효율적인 조합을 찾는 것은 정립되지 않음
Over-parameterization은 필요한 갯수보다 더 많은 parameter가 있다는 뜻, 이는 over-fitting을 유발하기 쉽다
3.Compound Model Scaling
1. Problem Formulation
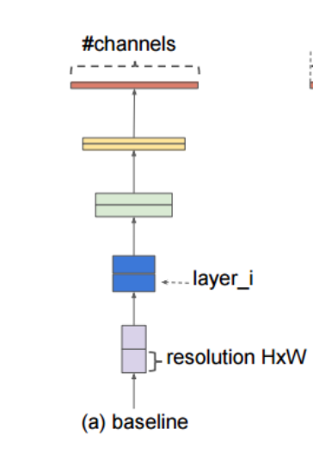
위 그림에서 입력값은 각 레이어 함수 f를 거쳐 최종 출력값을 생성하는데, 이를 수식으로 표현하면 아래의 식과 같다.

이를 일반화한 것이 아래 식인데, ConvNet을 수식화해 정리한 것이다.
H,W,C를 입력의 크기, F를 conv layer라고 하면 아래와 같이 표현할 수 있다.
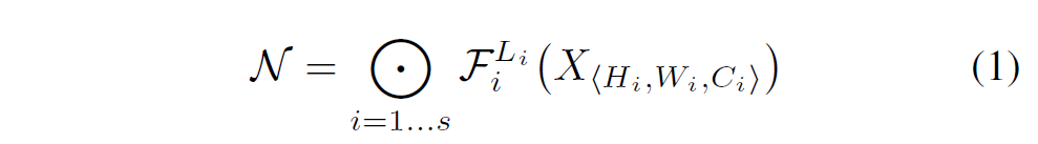
자원이 제한된 상태에서 정확도를 최대화하는 문제를 풀고자 하기 때문에, 이를 수식으로 정리하면 다음과 같다.
레이어 함수 f를 고정하고, 레이어 수 d, 채널 수 w, 입력 이미지 크기 r에만 집중하면 다음과 같은 수식이 된다.
이 w,d,r 간의 관계를 연구한 것이 EfficientNet 이다.
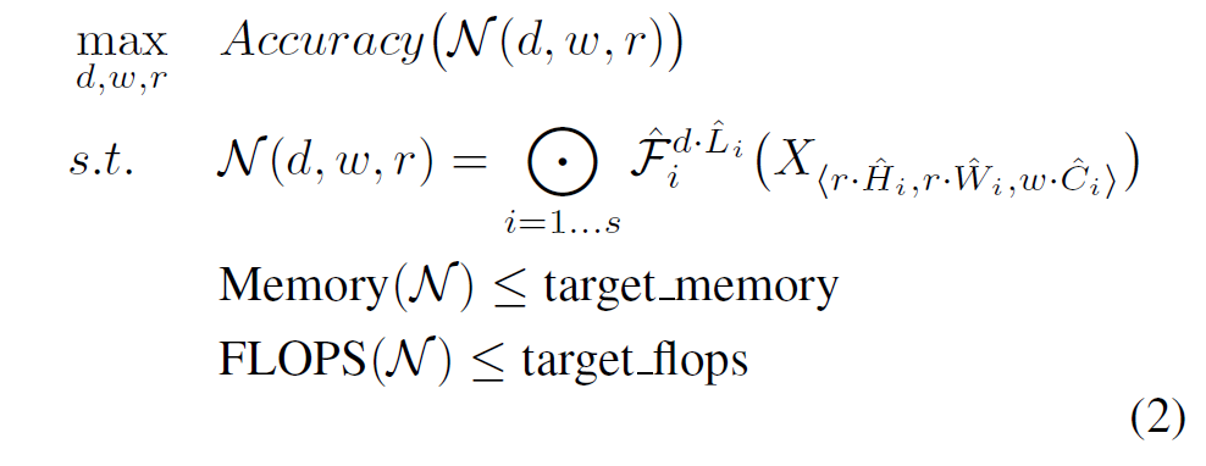
2. scaling Dimensions
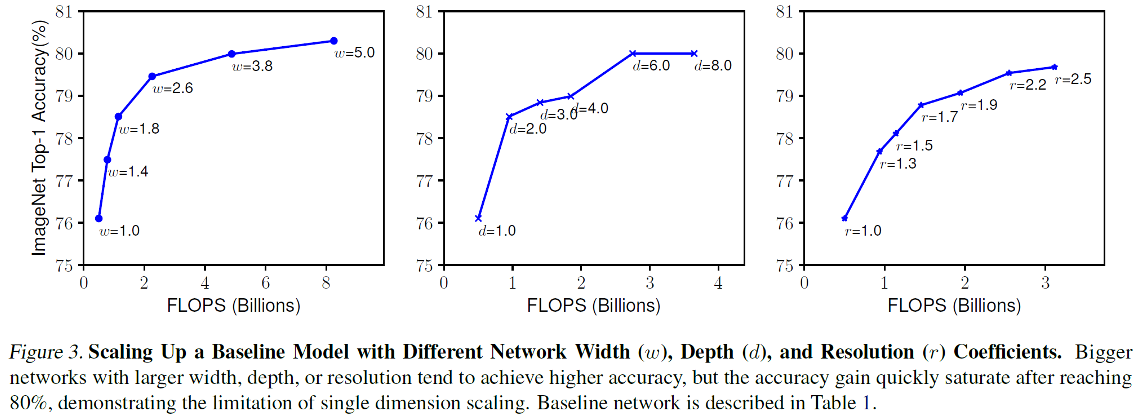
w(너비), d(깊이), r(입력 해상도)에 따른 정확도 값이다. 그림을 보면 w, d, r이 일정 값 이상이 되면 정확도가 빠르게 포화한다.
그리고, w, d, r이 낮을 때는 약간만 값을 조절해도 효과가 dramatic한 것을 확인할 수 있다.
그러나, 공통적으로, 어느 정도 이상 증가하면 모델의 크기가 커짐에 따라 얻는 정확도 증가량이 매우 적어지는 것을 알 수 있다.
3. Compound Scaling
=> w,d,r 값을 따로 조절하는 것이 아닌 함께 조절하여 최적의 효율을 찾아내는 것!
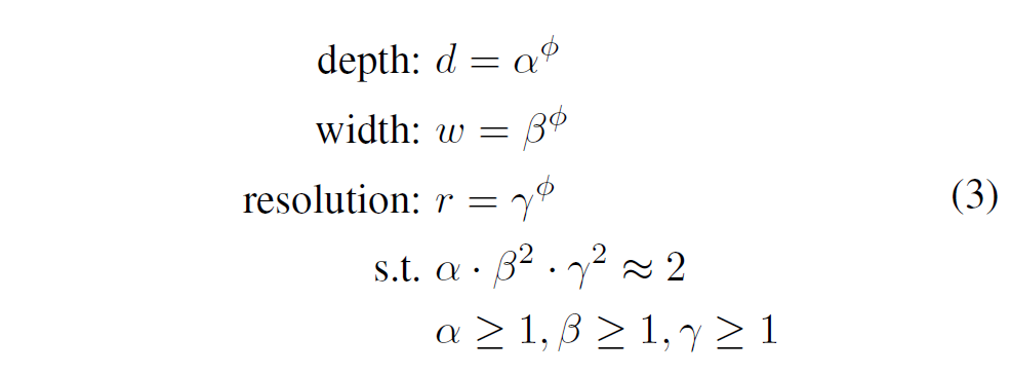
compound scaling 과정
STEP 1: ϕ=1로 고정 후, α,β,γ에 대해서 grid search를 수행 (
(grid search란, 해당 범위 및 step의 모든 경우의 수를 탐색하는 하이퍼파라미터 탐색 알고리즘)
(논문에서 찾은 값은 α=1.2,β=1.1,γ=1.15)
STEP 2: 이제 α,β,γ를 고정하고 ϕ를 변화시키면서 전체적인 크기를 키움 (B0~B7)
직관적으로, 더 높은 해상도의 이미지에 대해서는 네트워크를 깊게 만들어서 더 넓은 영역에 걸쳐 있는 feature(by larger receptive fields)를 더 잘 잡아낼 수 있도록 하는 것이 유리하다.
또, 더 큰 이미지일수록 세부적인 내용도 많이 담고 있어서, 이를 잘 잡아내기 위해서는 layer의 width를 증가시킬 필요가 있다.
FLOPs(초당 부동소수점 연산)는 너비와 해상도에 따라 제곱배가 상승한다. 너비를 2배 키우면 FLOPs는 4배가 증가하는 것.
따라서 FLOPs는 (α⋅β^2⋅γ^2)^2 배 만큼 증가합니다.
논문에서는 α⋅β^2⋅γ^2≈2로 제한하는데, 제한된 범위에서 α,β,γ를 찾는 것이다. 총 FLOPs는 2^ϕ 만큼 증가합니다.
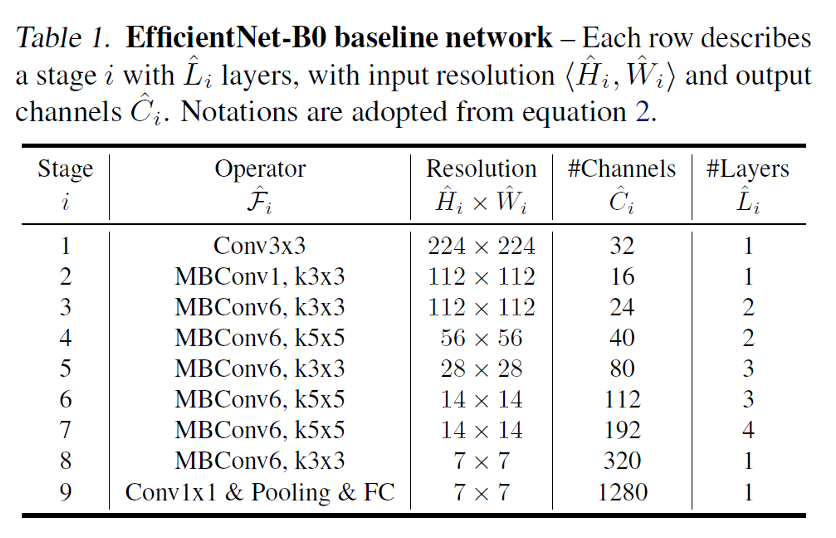
4.Architecture
MBConv는 MnasNet에서 사용하는 Conv 구조이다.

5. Experiment

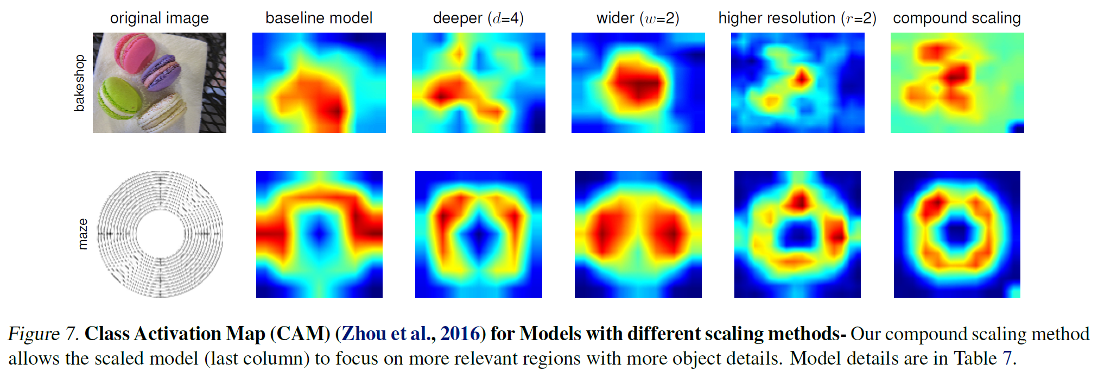
위 사진은 각 scaling 방법을 사용했을 때, 이미지의 어디에 집중하는지를 보여준다 (attention 사용은 x)
compound scaling이 좀 더 좋은 것을 알 수 있다.