Convolution 연산 이해하기
MLP와 달리, 커널(고정된 가중치 값)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조
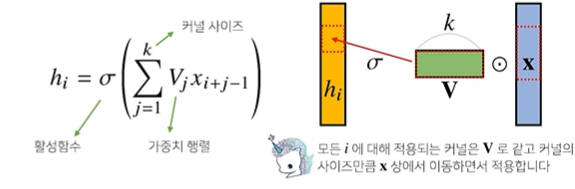
입력벡터 x를 모두 사용하는 것이 아니라, 커널 V의 사이즈 K만큼만 활용한다. -> 그래서 움직여가면서' 라는 표현을 사용
이 연산 역시도 선형변환에 속한다고 한다.
커널은 위 그림에서의 i와 상관없이 고정되므로, 파라미터 사이즈를 굉장히 많이 줄일 수 있다는 장점이 존재!
수학적 의미
신호를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링 하는 것
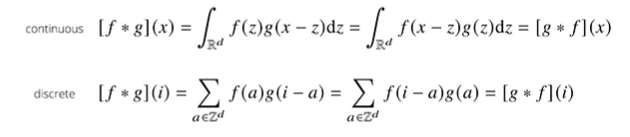
continuous할 때는 적분을 이용하고, discrete할 때는 급수로 표현한다. 하지만, 적용되는 방식은 동일하다.
즉, 두개의 함수 f와 g가 있을 때, 각각 z를 움직여가면서 적분을 하거나 더해주는 형태로 진행하게 된다.
f는 커널이고, g는 신호의 역할을 한다. x-z와 i-a는 신호 텀, z와 a는 커널 텀이다.
그러나, CNN에서 사용하는 연산은 엄밀히 말하면, 빼기(convolution)가 아니라 더하기(cross-correlation)를 사용한다.
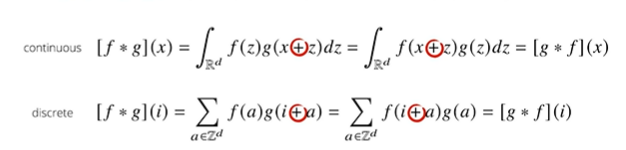
그렇지만, CNN이라 불렸던 이유는 역사적으로 그래왔기 때문이라고 한다..
영상처리에서 convolution
convolution연산에서 커널을 어떻게 설정하느냐에 따라 출력되는 결과물이 달라진다!


1차원뿐 아니라 다양한 차원에서도 계산이 가능하다.
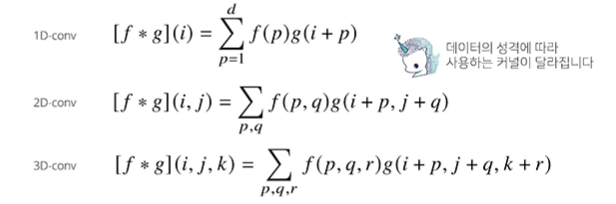
각 차원마다 차원에 맞는 좌표계를 이용한다 -> 차원이 높아진다고 해도 커널이 좌표의 위치에 따라 변하지는 앟는다!
p, q, r은 각각 x좌표 y좌표 z좌표라 생각하면 편하다.
※ 데이터의 성격에 따라 사용하는 커널이 달라진다!
2차원 convolution 연산 이해하기
행렬모양의 커널을 입력행렬 상에서 x,y방향으로 움직여가면서 선형모델과 합성함수가 적용되는 구조

커널과 입력의 연산은 element-wise이다!
출력의 크기 예상
입력(H,W)이고 커널 크기가 (KH,KW), 출력 크기를 (OH,OW)라 하면 출력 크기는 다음과 같다
OH = H - KH + 1
OW = W - KW +1
숫자로 예를 들면, 28x28입력을 3x3커널로 2D-conv 연산을 하면 26x26이 된다!
(26 = 28 - 3 + 1 이기 때문!)
채널이 여러개인 2차원 입력의 경우, 2차원 convolution을 채널 개수만큼 적용한다고 생각하면 된다.
RGB 같은 경우가 있다. 2차원이 입력이 여러 개라는 것은 3차원과 형태가 같음을 의미한다.
결국 근본은 2차원 convolution이므로, 2D conv를 진행해 주어야 한다.
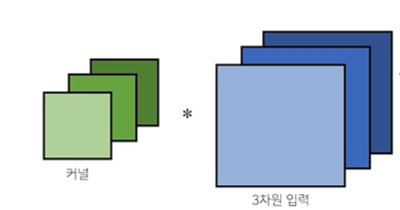
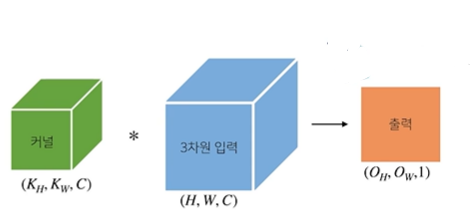
여러 채널이 존재하는 2차원 입력의 경우, 채널의 수 만큼 커널들을 만든 후 각각 연산을 수행한다. 그리고 각각의 연산결과를 전부 더하기 때문에 출력물의 3차원 값은 1이 되는 것이다.
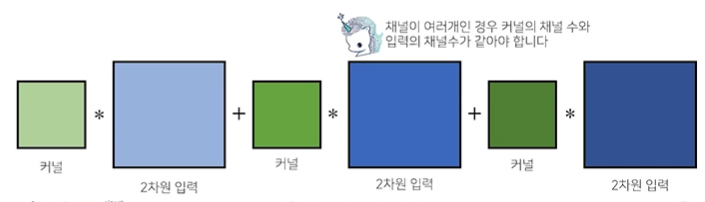
그렇다면 출력이 여러 채널을 가지게 하고 싶다면 어떻게 할까?
-> 커널의 개수를 늘리면 된다!
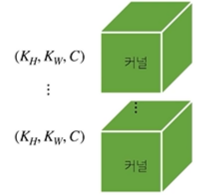
이렇게 커널의 개수를 Oc개만큼 사용한다면, 출력의 채널이 아래 사진과 같이 Oc개를 가지게 된다
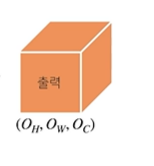
꼭 이런 형태가 아니더라도 여러 변형들이 존재한다고 한다. 그러나 위 그림들이 기본적인 CNN 모양이라고 한다.
convolution연산의 역전파
커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution연산이 나오게 된다

즉, convolution 연산에 미분을 해도 똑같이 convolution 연산이 나옴을 수식을 통해 확인할 수 있다.
그림을 통해 보자면,

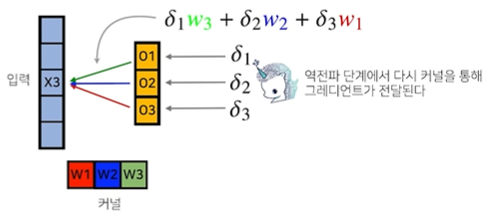
X3에서 출력을 결정할 때 각각 사용되는 가중치들이 있다. 바로 W1, W2, W2인데 X3에서 O1을 결정할 때 가중치 W3를 이용해 영향을 주었고, O2를 결정할 때는 W2를 이용해 영향을 주었다. 그리고 O3를 결정할 때는 W1을 이용해 영향을 주었다.
바로 위의 사진에서 왼쪽을 보면 알 수 있다. (X3로부터 뻗어나가는 화살표를 잘 살펴보자) / (X3 x W3 = O1 / X3 x W2 = O2 / X3 x W1 = O3)
역전파 단계에서는 출력 결정시에 사용된 가중치들과 δ값들을 곱해서 X3에 전달된다! (δ값들은 미분 값을 의미)
즉, 곱해졌던 커널들을 통해 그레디언트가 전달된다.
커널에는 어떻게 전파될까?

O3가 X3에 대해서 W1을 통해 그레디언트(δ3)를 전달했기 때문에, δ3 x X3는 W1의 그레디언트로 전달,
O2가 X3에 대해서 W2을 통해 그레디언트(δ2)를 전달했기 때문에, δ2 x X3는 W2의 그레디로 전달,
O1가 X3에 대해서 W3을 통해 그레디언트(δ1)를 전달했기 때문에, δ1 x X3는 W3의 그레디언트로 전달 되는 것이다.
각 커널에 들어오는 모든 그레디언트를 더하면, 결국 convolution 연산과 같다
'AI' 카테고리의 다른 글
| SegFormer custom data로 학습시키기! (1) | 2023.06.23 |
|---|---|
| RNN 첫걸음 (0) | 2022.09.28 |
| 딥러닝 기초 - RNN 간단 정리 (0) | 2022.09.28 |
| 딥러닝 기초 - CNN 간단 정리 (1) | 2022.09.28 |
| Regularization 간단 정리 (0) | 2022.09.28 |
