알고리즘/자료구조
에라토스테네스의 체 및 소수 구하기
beomseok99
2022. 7. 12. 01:01
728x90
에라토스테네스의 체(sieve of Eratosthenes)
= >N 이하의 소수(prime number)를 모두 정확히 찾아내는 도구
case1. O(N^2)
#include <cstdio>
#include <vector>
using namespace std;
const int MAX = 1000;
int main(){
vector<int> v;
for(int i=2; i<=MAX; i++){
bool isPrime = true;
for(int j=2; j<i; j++){
if(i%j == 0){
isPrime = false;
break;
}
}
if(isPrime) prime.push_back(i);
}
for(int i=0; i<v.size(); i++){
printf("%4d", v[i]);
if(i%10 == 9 || i == v.size()-1) puts("");
}
}case2. 에라토스테네스의 체 사용 -> O(n*log(log(n)))
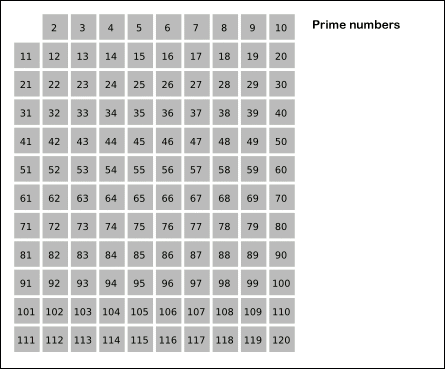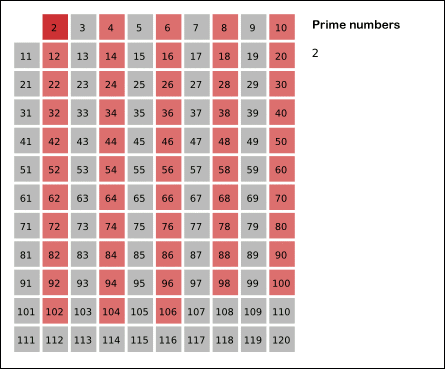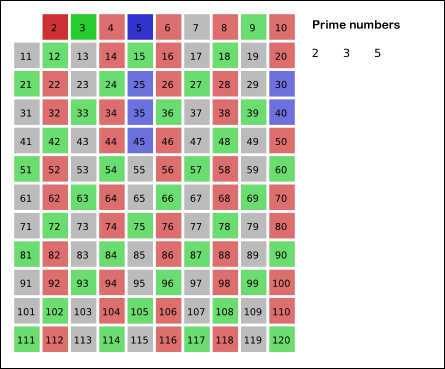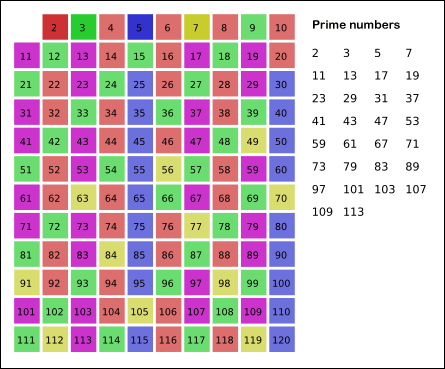
1. 2부터 시작해서 n까지 진행한다.
2. 가장 작은 수를 선택한다.
3. 선택된 가장 작은 수를 제외하고, 그 수의 배수들을 모조리 지운다.
#include<iostream>
#include<cmath>
using namespace std;
int main(){
int n = 1000;
int check[1001] = { false };
check[0] = check[1] = true;
for (int i = 2; i < 1000; i++){ // i < 1000/2 또는 sqrt(1000)으로 해도 ok!!
if (check[i] == false){
for (int j = i * 2; j <= 1000; j += i){ // int j= i*i로 시작해도 ok!!
check[j] = true;
}
}
}
for (int i = 1; i <= n; i++){
if (!check[i]) cout << i << '\n';
}
return 0;
}1000까지의 소수 판별을 하기 위해서는 1000의 제곱근까지만 진행해도 된다!
소수 구하기(prime number)
case1. 2부터 판별하는 수 전까지 나눠보고 나머지가 0이 안나온다면 소수로 정의
O(N)의 시간복잡도를 가짐,
int isPrime(int num){
for(int i=2; i<num; i++){
if(num % i == 0) return 0;
}
return 1;
}case2. 해당숫자의 절반까지만 확인하는 방법, 자기자신을 제외하고 절반을 초과하는 숫자에서 나눴을때 나머지가 0이되는 숫자는 나올수가 없다
마찬가지로 O(N)을 가진다.
int isPrime(int num){
for(int i=2; i<=num/2; i++){
if(num % i == 0) return 0;
}
return 1;
}case3. 해당 숫자의 √N 까지 확인하는 방법 = 약수의 중심을 구하는 방법
O(√N)의 시간복잡도를 가진다.
int isPrime(int num){
for(int i=2; i*i<=num; i++){
if(num % i == 0) return 0;
}
return 1;
}100을 예시로 들어보자
1 x 100, 2 x 50, 4 x 25, 5 x 20, 10 x 10, 20 x 5, 25 x 4, 50 x 2, 100 x 1
위와 같이 가운데 10 x 10을 중심으로 같은 연산이 반복된다.
때문에 제곱근(약수의 중심)까지만 연산을 진행해도 괜찮은 것이다.
728x90