https://www.acmicpc.net/problem/11657
11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
벨만-포드 알고리즘을 사용하는 문제이다.
그래프에서 음의 가중치가 등장한다면, 다익스트라로 해결할 수 없으므로 벨만-포드 알고리즘을 적용하자.
벨만 포드 알고리즘이란?
그래프의 최소비용을 구하는 알고리즘 중 하나로, "모든 경우의 수를 전부 탐색하여 최소비용을 찾는다." 자세히 말하자면, N개의 정점이 존재할 때 N-1번 탐색해야한다!
동작원리는 다음과 같다.
1. 모든 간선들을 탐색하면서, 해당 간선의 출발정점이 '한번이라도 계산 된 정점' 이라면 해당 간선의 도착정점이 가지고 있는 cost와, 출발한 정점의 비용 + 가중치값과 비교하여 최솟값을 업데이트 한다!
※ 한번이라도 계산(방문)된 정점이 아닐 때(=dist가 무한일 때)는 왜 무시를 할까?
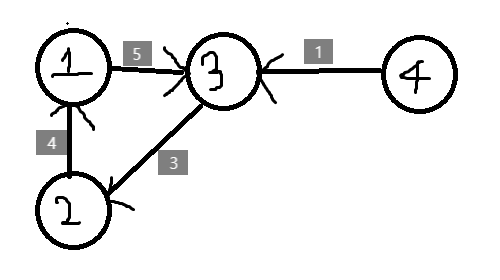
뭐 대충 이런 말도 안되는 그래프가 있다고 해보자.
만약 1->3으로 가는 가중치보다, 4->3으로 가는 가중치가 더 작다고 할 때, 방문하지 않은 노드에 대해서도 업데이트를 진행해주면, 도달할 수 없는 정점인 4번 정점을 포함하여 비용을 계산하게 된다.
이러한 것을 방지해주기 위해, dist가 무한이 아닌 출발정점에 대해서만 비용 계산을 진행해주는 것!
2. 1번 과정을 반복한다.
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<pair<pair<int,int>,int>> v;
int n,m,a,b,c;
long long dist[501];
void bellman_ford(){
dist[1]=0; // 1번 정점이 시작 정점이므로 비용 0으로 설정
for(int i=1;i<=n-1;i++){ // N-1번 반복
for(int j=0; j<v.size();j++){ // 한번 반복마다, 모든 간선에 대해 탐색
int start = v[j].first.first; // 출발정점
int End = v[j].first.second; // 도착정점
int cost = v[j].second; // 간선의 가중치
// 만약 출발하는 정점이 한번도 방문,계산되지 않은 정점이라면 패스
if(dist[start]==987654321) continue;
// 만약 도착정점의 비용이 출발정점의 비용 + 가중치보다 크다면
// 더 작은 값으로 업데이트
if(dist[End] > dist[start]+cost){
dist[End] = dist[start]+cost;
}
}
}
for(int i=0; i < v.size(); i++){ // 모든 간선 탐색
int start = v[i].first.first;
int End = v[i].first.second;
int cost = v[i].second;
if(dist[start]==987654321) continue;
// 정상적인 그래프(음의 사이클이 없는 그래프)라면 N-1번 탐색이 끝난 후에는,
// 더 탐색을 해도 비용이 바뀌면 안됨! -> 만약 바뀌면 음의 사이클 존재
if(dist[End] > dist[start]+cost){ // 비용이 바뀌면
cout << -1 <<'\n'; // 음의 사이클이 존재하므로 -1 출력하고 종료
return;
}
}
for(int i=2;i<=n;i++){ // 2번,3번, --- N번 정점까지의 비용 출력
if(dist[i]==987654321){ // 해당 정점으로 가는 경로가 없다면
cout << -1 << '\n';
}
else{
cout << dist[i] <<'\n';
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m;
for(int i=1; i<=n;i++) dist[i]=987654321; // 비용을 저장할 배열을 엄청 큰 값으로 초기화
for(int i=0; i<m;i++){
cin >> a >> b >> c;
v.push_back({{a,b},c}); // 출발정점, 도착정점, 가중치를 벡터에 저장
}
bellman_ford();
return 0;
}'알고리즘 > 백준(BOJ)' 카테고리의 다른 글
| [백준/C++] 2638번 치즈 (0) | 2022.09.29 |
|---|---|
| [백준/C++] 16954 움직이는 미로탈출 (0) | 2022.09.29 |
| [백준/C++] 17404번 RGB거리2 (0) | 2022.09.29 |
| [백준/C++] 6087번 레이저 통신 (0) | 2022.09.29 |
| [백준/C++] 1655번 가운데를 말해요 (0) | 2022.09.29 |
