728x90
선형 대수
1. scalar
- 숫자 하나
x = np.array(3)2. vector
- 숫자 여러개
x = np.arange(4)3. matrices
-2차원 행렬
x = np.arange(20).reshape(5,4)np.dot을 이용한 행렬 곱 가능
4. Tensor
- 3차원 이상
x = np.arange(24).reshape(2,3,4)np.dot 과 np.einsum으로 텐서 곱 가능
5. Norm

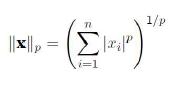
미분

미분의 정의
미분을 통해 접선의 기울기를 구할 수 있다
-> 또한 어느 방향으로 이동해야 함수값이 증가하는지 / 감소하는지 알 수 있다!
함수값 증가 : 미분값을 더해준다 => 경사상승법 (함수의 극대값의 위치를 구할 때 사용)
함수값 감소 : 미분값을 빼준다 => 경사하강법 (함수의 극소값의 위치를 구할 때 사용)
두 방법 모두 극값에 도달하면 움직임을 멈춘다!
기초 미분 공식
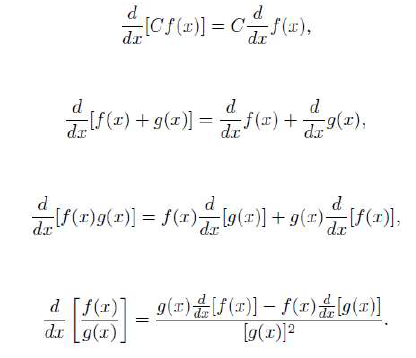
기초 미분
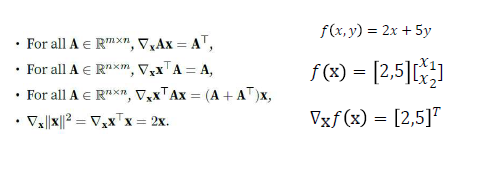
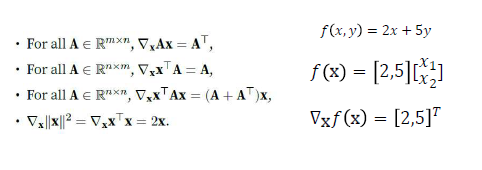
파이썬 코드로 미분
- sympy 모듈 활용
import sympy as sym from sympy.abc import x sym.diff(sym.poly(x**2 + 2*x + 3), x)- 편미분
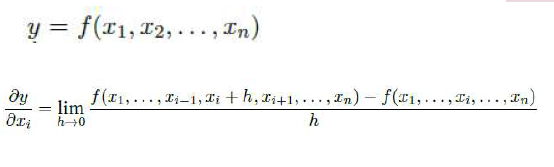
벡터가 입력인 다변수 함수의 경우 편미분을 사용한다.
주어진 변수의 개수만큼 편미분 가능
import sympy as sym
from sympy.abc import x,y
sym.diff(sym.poly(x**2 + 2*x*y + 3) + sym.cos(x + 2y),x) # x에 대해 편미분- Gradient
각 변수별로 편미분을 계산한 gradient 벡터를 이용하여 경사하강/상승법에 사용할 수 있다.
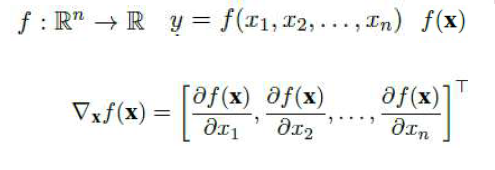
그레디언트 벡터는 각 점(x,y)에서 가장 빨리 증가하는 방향으로 흐르게 된다!
마이너스를 붙여주면, 각 점에서 가장 빨리 감소하게 되는 방향으로 흐른다!
-> 최솟값을 구해 최적화 가능!
그래디언트 예시
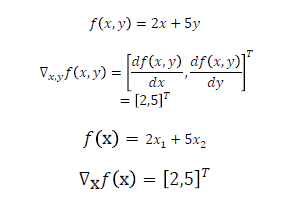
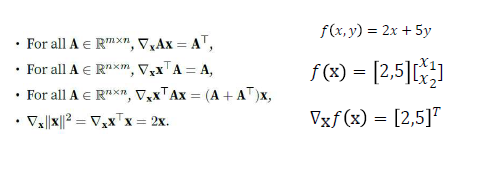
경사하강법 알고리즘 (최적화 알고리즘)
var = init # init = 시작점
grad = gradient(var) # gradient는 미분 계산하는 함수
while(abs(grad) > eps) : # eps는 알고리즘 종료조건인데,
# while(norm(grad) > eps) : 벡터는 절대값을 구할 수 없으므로 노름(norm)을 사용하여 종료조건을 설정
# 컴퓨터에서는 미분값이 0이 나오지 않으므로 작거나 같아지면 종료하도록 함
var = var - lr * grad # lr은 학습률
grad = gradient(var)
- Chain rule
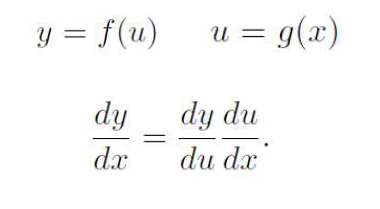
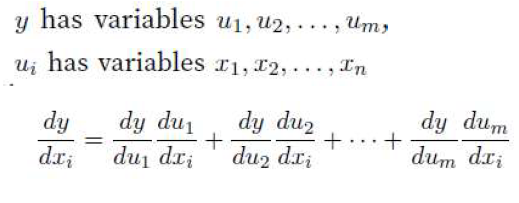
728x90
'수학 > 선형대수학' 카테고리의 다른 글
| 벡터와 행렬 간단 정리 (0) | 2022.09.28 |
|---|