https://www.acmicpc.net/problem/1111
1111번: IQ Test
다음 수를 출력한다. 만약 다음 수가 여러 개일 경우에는 A를 출력하고, 다음 수를 구할 수 없는 경우에는 B를 출력한다.
www.acmicpc.net
문제를 보면, 다음 수는 이전 수 * a + b이다.
이걸 잘 풀어보면 y = ax + b인 방정식으로 풀 수 있다. 여기서 x는 이전 수이고, y는 현재 수이다.
만약 아래와 같이 입력이 들어온다면, 2 = 1 * a + b인 것이다. 그렇다면 2를 f(1)로 표현할 수 있다!
5
1 2 3 4 5
여기서 a는 직선의 기울기를 의미하게 되는데, 기울기를 구하는 공식은 다음과 같다.
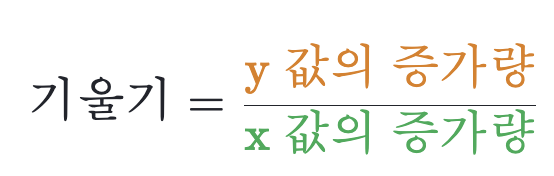
즉, f(2) - f(1) / 2 - 1 로 구할 수 있고, f(a)는 3이고 f(1)은 2 이므로 결국 예시에서의 기울기는 1이다.
y절편은 원래는 x에 0을 넣어서 구하지만, 이 문제에서는 다르게 구했다. 앞서 구한 기울기를 이용하면,
y = 1 * x + b 가 된다. 이는 f(x) = x + b와 동일하고, 위 예제의 숫자를 넣어보면 다음과 같다.
2 = 1 * 1 + b 가 된다. 이제 y절편인 b를 구할 수 있다.
또한, N==1, N==2, N==3 일 때 경우를 잘 따져서 구분해주면 된다.
import sys
#sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def get_A(i):
if numbers[i]-numbers[i-1] == 0: return 1
return int((numbers[i+1]-numbers[i]) / (numbers[i]-numbers[i-1])) # 기울기 공식 f(a)-f(b) / a-b
def get_B(i,a):
return int(numbers[i] - a * numbers[i-1]) # y절편
def isEqual(x):
return len(set(x)) <= 1
if __name__ == "__main__":
N = int(input())
numbers = list(map(int, input().split()))
if N == 1: print('A')
elif N == 2:
if numbers[0] == numbers[1]: print(numbers[1])
else:
print('A')
else: # N==3
if isEqual(numbers):
print(numbers[0])
else:
for i in range(1,N-1):
a = get_A(i)
b = get_B(i,a)
end = False
flag = True
for idx in range(1,N):
if numbers[idx] != (numbers[idx-1] * a + b) :
flag = False
break
if flag:
print(int(numbers[-1] * a + b))
end = True
break
if not end: print('B')'알고리즘 > 백준(BOJ)' 카테고리의 다른 글
| [백준/파이썬] 1041번 주사위 (0) | 2023.05.31 |
|---|---|
| [백준/파이썬] 12919번 A와 B 2 (0) | 2023.05.27 |
| [백준/파이썬] 17144번 미세먼지 안녕! (0) | 2023.05.04 |
| [백준/파이썬] 2877번 4와 7 (0) | 2023.04.26 |
| [백준/파이썬] 2108번 통계학 (0) | 2023.03.30 |
https://www.acmicpc.net/problem/1111
1111번: IQ Test
다음 수를 출력한다. 만약 다음 수가 여러 개일 경우에는 A를 출력하고, 다음 수를 구할 수 없는 경우에는 B를 출력한다.
www.acmicpc.net
문제를 보면, 다음 수는 이전 수 * a + b이다.
이걸 잘 풀어보면 y = ax + b인 방정식으로 풀 수 있다. 여기서 x는 이전 수이고, y는 현재 수이다.
만약 아래와 같이 입력이 들어온다면, 2 = 1 * a + b인 것이다. 그렇다면 2를 f(1)로 표현할 수 있다!
5
1 2 3 4 5
여기서 a는 직선의 기울기를 의미하게 되는데, 기울기를 구하는 공식은 다음과 같다.
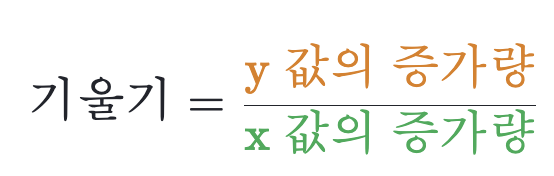
즉, f(2) - f(1) / 2 - 1 로 구할 수 있고, f(a)는 3이고 f(1)은 2 이므로 결국 예시에서의 기울기는 1이다.
y절편은 원래는 x에 0을 넣어서 구하지만, 이 문제에서는 다르게 구했다. 앞서 구한 기울기를 이용하면,
y = 1 * x + b 가 된다. 이는 f(x) = x + b와 동일하고, 위 예제의 숫자를 넣어보면 다음과 같다.
2 = 1 * 1 + b 가 된다. 이제 y절편인 b를 구할 수 있다.
또한, N==1, N==2, N==3 일 때 경우를 잘 따져서 구분해주면 된다.
import sys
#sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def get_A(i):
if numbers[i]-numbers[i-1] == 0: return 1
return int((numbers[i+1]-numbers[i]) / (numbers[i]-numbers[i-1])) # 기울기 공식 f(a)-f(b) / a-b
def get_B(i,a):
return int(numbers[i] - a * numbers[i-1]) # y절편
def isEqual(x):
return len(set(x)) <= 1
if __name__ == "__main__":
N = int(input())
numbers = list(map(int, input().split()))
if N == 1: print('A')
elif N == 2:
if numbers[0] == numbers[1]: print(numbers[1])
else:
print('A')
else: # N==3
if isEqual(numbers):
print(numbers[0])
else:
for i in range(1,N-1):
a = get_A(i)
b = get_B(i,a)
end = False
flag = True
for idx in range(1,N):
if numbers[idx] != (numbers[idx-1] * a + b) :
flag = False
break
if flag:
print(int(numbers[-1] * a + b))
end = True
break
if not end: print('B')'알고리즘 > 백준(BOJ)' 카테고리의 다른 글
| [백준/파이썬] 1041번 주사위 (0) | 2023.05.31 |
|---|---|
| [백준/파이썬] 12919번 A와 B 2 (0) | 2023.05.27 |
| [백준/파이썬] 17144번 미세먼지 안녕! (0) | 2023.05.04 |
| [백준/파이썬] 2877번 4와 7 (0) | 2023.04.26 |
| [백준/파이썬] 2108번 통계학 (0) | 2023.03.30 |