https://www.acmicpc.net/problem/17071
17071번: 숨바꼭질 5
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 500,000)에 있고, 동생은 점 K(0 ≤ K ≤ 500,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때
www.acmicpc.net
숨바꼭질 시리즈의 최종판이다.
이 문제는 다른 문제들과 달리, 동생의 위치에 포커싱을 맞춰야한다. (1초에는 1만큼 움직이고, 2초에는 2만큼 움직인다) (즉, 움직인 거리로 시간을 대체할 수 있다!)
만약 수빈이가 14초에 x라는 지점을 방문했다고 하자. 그런데 동생이 20초에 그 x지점을 방문했다.
그럼 수빈이와 동생은 20초만에 만날 수 있는 것이다. 라는게 이 문제의 풀이법인데 처음엔 이게 뭔 뚱딴지 같은 소린가 싶었다.
해석 => 수빈이는 14초에 x에 방문했다. 수빈이는 -1과 +1, *2의 위치로 이동할 수 있으므로 15초에는 -1 움직여서 x-1로 방문했다고 하자. 그런 다음 16초에 +1 움직이면 다시 x로 돌아올 수 있다!! (이게 중요) 이렇게 계속 반복하면 수빈이는 14, 16, 18초에도 x에 위치할 수 있고 결국 20초에 동생과 만날 수 있는 것이다.
홀수의 경우도 동일하다. 13초에 x에 방문했다고 하면 15, 17, ... 초에 계속 x에 위치할 수 있는 것이다.
동생의 위치가 500,000보다 커지면 만날 수 없는 것이고, %2 연산을 통해 동생이 방문한 곳을 수빈이가 방문했다면 그곳이 답이다.
bfs에서 큐 사이즈를 이용하는 방식은 약간의 테크닉으로, bfs에서 깊이의 수를 셀 때 사용한다.
이 문제에서 bfs의 깊이 1은 1초를 의미하기 때문에 해당 방법과 같은 문제로 풀이하였다.
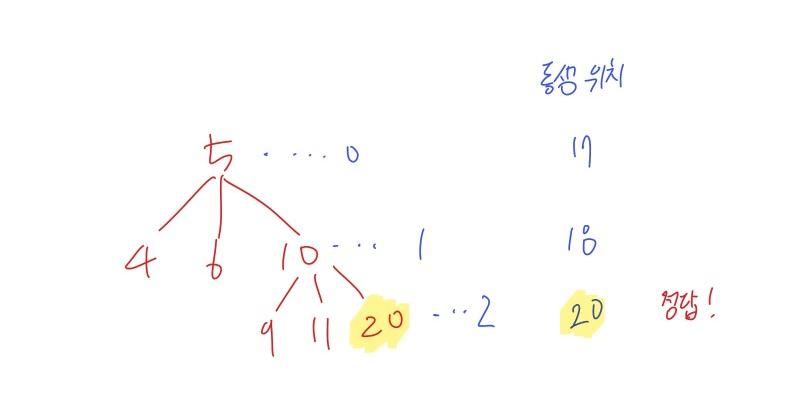
* depth가 1 내려갈 때 마다 x에 대해서 x-1, x+1, x*2를 탐색하는 것을 유의! 문제의 두번째 예시인 17 5에 대한 그래프를 전부 그려보면 바로 이해가 될 것이다.
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
int n,k,mov=1;
int ans = -1;
queue<int> q;
bool visited[2][500001];
void bfs(){
while (!q.empty()) {
k += mov;
if(k> 500000) {
ans = -1;
return;
}
if (visited[mov % 2][k]) {
ans = mov;
return;
}
int siz = q.size();
for (int i = 0; i < siz; i++) {
int x = q.front();
q.pop();
for (int nx : {x - 1, x + 1, 2 * x}) {
if (nx == k) {
ans = mov;
return;
}
if (nx < 0 || nx>500000) continue;
if (visited[mov % 2][nx]) continue;
visited[mov % 2][nx] = true;
q.push(nx);
}
}
mov++;
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> k;
if (n == k) {
cout << 0;
return 0;
}
q.push(n);
bfs();
cout << ans;
return 0;
}'알고리즘 > 백준(BOJ)' 카테고리의 다른 글
| [백준/C++] 1305번 광고 (0) | 2022.11.27 |
|---|---|
| [백준/C++] 1377번 버블 소트 (0) | 2022.11.24 |
| [백준/C++] 12851번 숨바꼭질 2 (0) | 2022.11.19 |
| [백준/C++] 1697번 숨바꼭질 (0) | 2022.11.15 |
| [백준/C++] 15683번 감시 (0) | 2022.11.14 |
https://www.acmicpc.net/problem/17071
17071번: 숨바꼭질 5
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 500,000)에 있고, 동생은 점 K(0 ≤ K ≤ 500,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때
www.acmicpc.net
숨바꼭질 시리즈의 최종판이다.
이 문제는 다른 문제들과 달리, 동생의 위치에 포커싱을 맞춰야한다. (1초에는 1만큼 움직이고, 2초에는 2만큼 움직인다) (즉, 움직인 거리로 시간을 대체할 수 있다!)
만약 수빈이가 14초에 x라는 지점을 방문했다고 하자. 그런데 동생이 20초에 그 x지점을 방문했다.
그럼 수빈이와 동생은 20초만에 만날 수 있는 것이다. 라는게 이 문제의 풀이법인데 처음엔 이게 뭔 뚱딴지 같은 소린가 싶었다.
해석 => 수빈이는 14초에 x에 방문했다. 수빈이는 -1과 +1, *2의 위치로 이동할 수 있으므로 15초에는 -1 움직여서 x-1로 방문했다고 하자. 그런 다음 16초에 +1 움직이면 다시 x로 돌아올 수 있다!! (이게 중요) 이렇게 계속 반복하면 수빈이는 14, 16, 18초에도 x에 위치할 수 있고 결국 20초에 동생과 만날 수 있는 것이다.
홀수의 경우도 동일하다. 13초에 x에 방문했다고 하면 15, 17, ... 초에 계속 x에 위치할 수 있는 것이다.
동생의 위치가 500,000보다 커지면 만날 수 없는 것이고, %2 연산을 통해 동생이 방문한 곳을 수빈이가 방문했다면 그곳이 답이다.
bfs에서 큐 사이즈를 이용하는 방식은 약간의 테크닉으로, bfs에서 깊이의 수를 셀 때 사용한다.
이 문제에서 bfs의 깊이 1은 1초를 의미하기 때문에 해당 방법과 같은 문제로 풀이하였다.
* depth가 1 내려갈 때 마다 x에 대해서 x-1, x+1, x*2를 탐색하는 것을 유의! 문제의 두번째 예시인 17 5에 대한 그래프를 전부 그려보면 바로 이해가 될 것이다.

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
int n,k,mov=1;
int ans = -1;
queue<int> q;
bool visited[2][500001];
void bfs(){
while (!q.empty()) {
k += mov;
if(k> 500000) {
ans = -1;
return;
}
if (visited[mov % 2][k]) {
ans = mov;
return;
}
int siz = q.size();
for (int i = 0; i < siz; i++) {
int x = q.front();
q.pop();
for (int nx : {x - 1, x + 1, 2 * x}) {
if (nx == k) {
ans = mov;
return;
}
if (nx < 0 || nx>500000) continue;
if (visited[mov % 2][nx]) continue;
visited[mov % 2][nx] = true;
q.push(nx);
}
}
mov++;
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> k;
if (n == k) {
cout << 0;
return 0;
}
q.push(n);
bfs();
cout << ans;
return 0;
}'알고리즘 > 백준(BOJ)' 카테고리의 다른 글
| [백준/C++] 1305번 광고 (0) | 2022.11.27 |
|---|---|
| [백준/C++] 1377번 버블 소트 (0) | 2022.11.24 |
| [백준/C++] 12851번 숨바꼭질 2 (0) | 2022.11.19 |
| [백준/C++] 1697번 숨바꼭질 (0) | 2022.11.15 |
| [백준/C++] 15683번 감시 (0) | 2022.11.14 |
